Saudações leitores,
A fim de avaliar as
tensões de flexão em barras, a equipe utilizará uma ponte de Wheatstone. Sendo
assim, é necessário, primeiramente, entender o que é e como funciona a ponte
para então saber aplicá-la da forma correta a atender nosso objetivo.
A ponte de Wheatstone é um circuito composto por 4 resistores, sendo dois conjuntos em paralelo de 2 resistores em série. Em paralelo com esses conjuntos é conectado um galvanômetro. A Figura 1 representa uma ponte de Wheatstone.
Figura 1: Ponte de Wheatstone
Fonte: YOUNG, 2009, p. 199
A primeira lei de Kirchhoff, chamada de lei das malhas, foi introduzida no Capítulo 24. Esta lei segue diretamente da presença de um campo conservativo
 .* Dizer que um campo é conservativo
significa dizer que
.* Dizer que um campo é conservativo
significa dizer que
onde a integral é calculada em qualquer curva
fechada C. As variações no potencial e
e estão relacionados por
estão relacionados por . Portanto, a Equação
25-27 significa que a soma das variações no potencial (a soma dos
. Portanto, a Equação
25-27 significa que a soma das variações no potencial (a soma dos ) em qualquer
trajetória fechada é igual a zero. (TIPLER, 2009)
) em qualquer
trajetória fechada é igual a zero. (TIPLER, 2009)
 e
e estão relacionados por
estão relacionados por . Portanto, a Equação
25-27 significa que a soma das variações no potencial (a soma dos
. Portanto, a Equação
25-27 significa que a soma das variações no potencial (a soma dos ) em qualquer
trajetória fechada é igual a zero. (TIPLER, 2009)
) em qualquer
trajetória fechada é igual a zero. (TIPLER, 2009)
A segunda lei de Kirchhoff, chamada de lei dos nós,
segue da conservação de carga. A figura 25-26 mostra a junção dos fios
conduzindo correntes I1, I2 e I3. Como a carga não é criada nem acumulada neste ponto,
a conservação de carga conduz à lei dos nós que, para este caso, é
(TIPLER, 2009)
Para cada conjunto, a resistência de cada um desses
resistores pode ser conhecida com precisão. Com as chaves K1 e K2
fechadas, fazemos variar essas resistências até que a corrente indicada no
galvanômetro seja igual a zero; dizemos, então, que a ponte está equilibrada. (YOUNG, 2009)
Analisando a Figura 1 e aplicando a segunda lei de
Kirchhoff, é possível concluir que a corrente que passa no trecho ab é a mesma
que passa no trecho bd; analogamente, a corrente que passa no trecho ac é a
mesma que passa no trecho cd. Aplicando a primeira lei de Kirchhoff, têm-se
Se (3) for satisfeita, a ponte está em equilíbrio.
Para verificar essa condição, nosso professor de Física C prática, Targino
Amorim, nos desafiou a montar uma ponte utilizando uma placa de montagem, uma
fonte de tensão variável, um multímetro, 4 resistores com lâmpadas acopladas e
cabos para ligação. Após a montagem, ligamos a ponte numa fonte de 10V e foi
possível ver as lâmpadas acesas. A tensão medida com o multímetro marcava zero
e a lâmpada do resistor ligado em paralelo com o multiteste não acendeu. Com
isso, concluímos que a ponte estava equilibrada. Na Figura 2 e 3, pode-se ver os dois circuitos
montados pela equipe.
Figura 2: Circuito I
Fonte: Própria
Figura 3: Circuito II
Fonte: Própria
Bem, agora que já sabemos o que é e como funciona a
ponte de Wheatstone, é possível adapta-la ao nosso projeto. Nele, iremos
substituir dois resistores de intensidade conhecida por um extensômetro e um
resistor variável. Quando a barra fletir, o extensômetro terá seu comprimento
alongado, e consequentemente, o valor da sua resistência mudará. Com o auxilio
do resistor variável, podemos ajustar sua resistência até a tensão indicada no
multiteste ser zero, equilibrando desta forma a ponte. Na figura 4 podemos ver
a representação da ponte de Wheatstone que será utilizada no projeto, onde o R1
é um resistor variável.
Figura 4: Ponte de Wheatstone utilizada no projeto
Fonte: https://morf.lv/strain-gauge-based-weight-sensor-load-cell
Postado por Pedro de Alcantara Almeida Neto

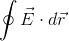












Preciso de uma ponte de wheatstone urgente em Belo Horizonte. Obrigada, era o que eu procurava
ResponderExcluir